 2025.10.02
2025.10.02
はじめに
例えばサイト内バナーのCTRを計測したとき、出てきた数値がどれくらい信用できるかを確かめるために二項分布というものを使うと思います。
数学の授業でちょっと触った記憶がある人もいるかもしれません。
データ分析をしていると統計学に触れることが多々あるのですが、その時に”負の”二項分布という概念に出会うことがあります。
書籍やサイトを見ているとよく袋から玉を取り出す試行を例にとって説明がされるイメージがありますが、生きててあまり袋から玉を取り出した経験がないため「こんなことをして何になるんだろう?」みたいなことをよく考えてしまっていました。
また実務への応用方法についてもよく分からないままここまで来てしまったので、基本から学び直してWebマーケティング分野での利用方法を考えることでデータ分析の武器にしたい!!
…ということでしばしお付き合いください。
この記事では必要最低限の式を除いて、出てくる概念の数理的な解釈とかは行わないつもりなのでご了承ください。
そもそも二項分布とは?
いったん二項分布の復習です。読まなくてもいいです笑
サイト上にとあるバナーがあって、潜在的に0.3(30%)のCTRを生む能力があるとします。
つまり1回のインプレッションが発生した時に、ユーザーは7割の確率でクリックしないし、3割の確率でクリックします。
これを繰り返したとき、結果としてデータに出てくるCTRが描く分布のことを二項分布と言います。
同じバナーを同じ場所に同じような時期に設置しても、運やその他の要因によってその時々でCTRがバラけることは想像に難くないと思います。そのバラけ具合を計算したものが二項分布です。
グラフにするとこんな感じ。
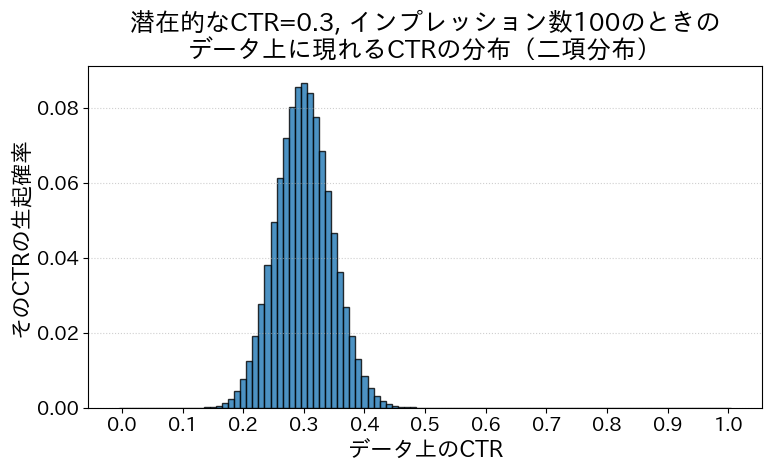
このバナーは能力としては3割くらいクリックを獲得する力があるのに、偶然クリックされないことが続くとデータとして現れるCTRは25%になったり、逆に確率はあまり多くないですが偶然によって40%を超えたりもするということです。
二項分布を数式で表すと以下の通りです。
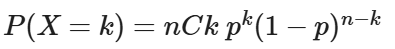
データ上でクリック数がkとなる確率。nがインプレッション数、kがデータ上に現れるクリック数、pが潜在的なCTRの能力です。
ですのでたとえば、100インプレッションでCTRが30%と出たとしても、「いやいやこの場合10%という少ない確率ではあるけどCTRが25%を下回ることもありうるよね。もうちょっとインプレッション増やして確度高めた方がいいよね」みたいな議論になるわけです。
負の二項分布とは?
それでは”負の”二項分布は何を指すのでしょうか?例を二つ紹介します。
バナーとCTRの例では、さっきと同じように0.3のCTRを潜在的に持つバナーを考えます。
最初のインプレッションでは7割の確率でクリックをされないこのバナーですが、何回も見られたらそのうちクリックされるだろうな、というのはご想像つきやすいと思います。
この時、「合計で5回クリックが発生するまでに、何回失敗があったか?」というのを表すのが負の二項分布です。
また、よく見かける例として、袋に入った玉を使った例もご紹介します。
袋にハズレの青い玉を5個、アタリの白い玉を2個入れます。今この袋から適当に玉を一つ取り出して、ハズレかアタリかを見てから袋に戻すという動作を考えましょう。
都度初期条件に戻しているので、アタリを引く確率は毎回 2/(2+5) ≒ 0.3くらいです。同じように、「合計で3回アタリを引くまでに、何回ハズレを引いたか?」というのを表すのが負の二項分布ということになります。
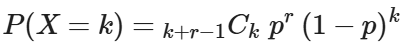
負の二項分布の式:r回成功するまでの失敗回数がkとなる確率。データ上では総インプレッション数がr+kとなります。
Webマーケティングでの使い道を考える①
「じゃあ、これの何が嬉しいの??」ということを考えたいです。ここからは主観に基づく推測が多分に含まれるので、ご理解のほどお願いいたします。
先ほど出てきたバナーのCTRを例に挙げると、目標が100回のクリック保証型広告の総インプ数は負の二項分布に従いそうです。
まず、掲載枠の位置・クリエイティブや文言が類似した従来のバナーでの成績などと照らし合わせておおよそのCTRを算出します。
ここではさっきと同じようにCTR=0.3として、目標クリック数を100回としましょう。
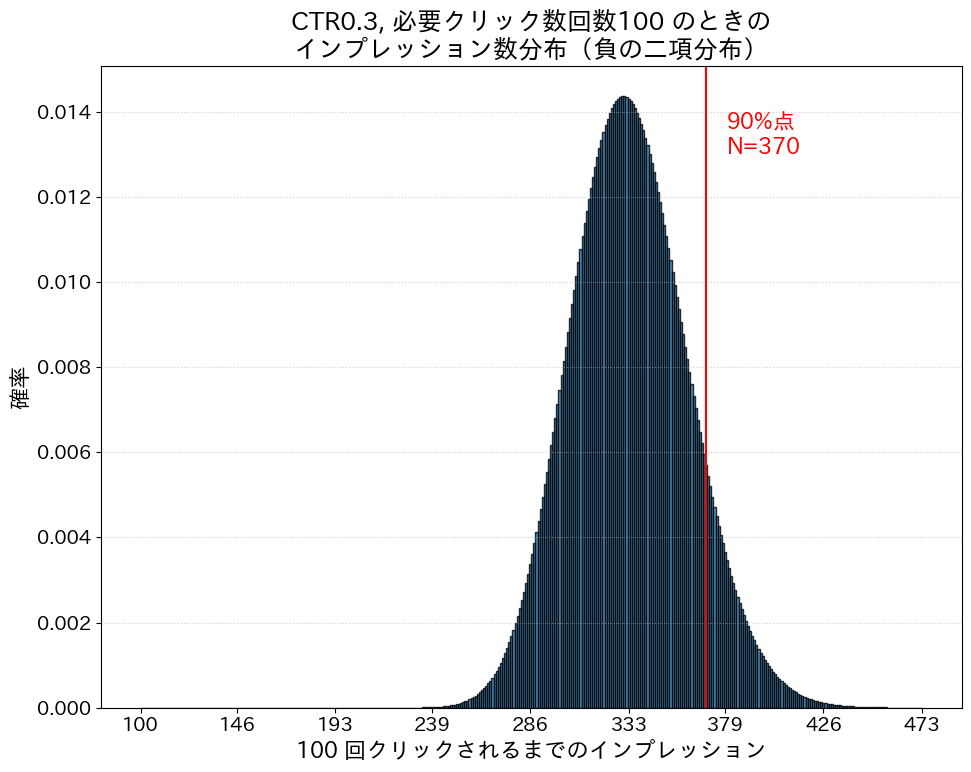
普通に計算すると100回/0.3≒333で340回くらいがインプレッション数の期待値となりますが、負の二項分布に基づいてインプレッション総数の生起確率を計算したものが以下のグラフです。なお、ここでは失敗した試行と成功した試行を合わせてインプレッションとしていることにご留意ください。

大体9割くらいの打率で安全に100回クリック確保できるだろうというインプレッション数は370となりました。思ったより多かったでしょうか?予想通りでしょうか?
実務上のCTRはもっとずっと小さくなりがちですし、期待値と9割安全ラインの開きは更に大きくなると予想できます。
ボーダーをどこに定めるかは決めの問題とはなってしまいますが、広告予算の設定や在庫管理などに応用できそうな気がします。
また、インプレッション数の予測を定量的に行うことで「インプレッションの期待値は340弱だけど、とりあえず余裕持って400くらい見ておくか~」という判断における無駄を省くこともできそうです。
Webマーケティングでの使い道を考える②
一定期間内に特定の商品をn回買うユーザー数の分布を、その商品が市場全体においてどのくらい好まれているか(プレファレンス)を用いて表したNBDモデルというマーケティングモデルがあります。
これは森岡毅氏『確率思考の戦略論』で提唱されている概念であり詳しくは書籍を読んでいただければと思うのですが、たとえば2週間あたり1000世帯におけるパンケーキの購入回数分布(未購入の世帯が○○%, 2回購入した世帯が△%など)をかなり高い精度で予測しています。
単位時間当たりの購入回数ならあるいはポアソン分布では?とも考えてしまいますが、「商品を1回買えばその次も同じ商品を選好する確率が増える」ということを加味すると負の二項分布を拡張した数式モデルとなるみたいだという理解をしました。
実際期待値と分散が同じポアソン分布と比べると、負の二項分布の方がデータの分散が大きい場合には有効なようです。
上記の場合のほか、地域ごとの差異が大きくて全体の分散が大きくなるデータなど不均一な集団においてはポアソン分布より負の二項分布の方が柔軟に適応できるみたいです。この辺りは業務で使用しつつ考えてみるのが良さそうだと感じました。
CVや特定の回数をユーザーごとに追いたいとき、サンプルの性質を考慮してからポアソン分布と負の二項分布を使い分けるのが有効な手立てといったところでしょうか。
おわりに
今回ご紹介したのはごく一部の使い方に過ぎないとは思いますが、「過度に大きな分散に強い」という特徴はさまざまなケースで応用が効きます。
また、バナーCTRなど身近な例に置き換えることで多少は理解が進みました。
より説得力のある分析や余裕ある計画立案のため、知識を消化して積極的にアウトプットに活かしたいと思います。